
Rha Overstreet - PharaohSun
# Importing libraries
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from statsmodels.formula.api import ols as sm_ols
from statsmodels.iolib.summary2 import summary_col # nicer tables
# Reading in dataset
df = pd.read_csv('input_data2/housing_train.csv')
Part 1: EDA
Simple EDA
def edaSimple(df):
numerics = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
numeric_variables = df.select_dtypes(include=numerics).columns
categorical_variables = df.drop(numeric_variables, axis = 1).columns
dataShape = df.shape
num_unique = df[numeric_variables].nunique()
cat_unique = df[categorical_variables].nunique()
units_of_observation = ['v_SalePrice', 'v_Year_Built','v_Yr_Sold','v_Mo_Sold', 'v_Lot_Area']
print("There are", df.shape[0], "observations and", df.shape[1], "variables.", "\n",
"The build dates range from", df.v_Year_Built.min(), "to", df.v_Year_Built.max(), "\n",
"The sale dates range from", df.v_Yr_Sold.min(), "to", df.v_Yr_Sold.max(), "\n")
print("The shape of the data is", "\n", dataShape, "\n",
"Numeric Variables", "\n", numeric_variables , "\n",
"Categorical Variables", "\n", categorical_variables , "\n",
"Number of unique numerical variables", "\n", num_unique , "\n",
"Number of unique categorical variables", "\n", cat_unique , "\n",
"Main units of observation", "\n", df[units_of_observation].describe(), "\n",
"Categorical variable counts", "\n")
for var in categorical_variables:
print(var, "| Note: limited to top 5 values.")
print(df[var].value_counts().head(5), '\n---')
edaSimple(df)
There are 1941 observations and 81 variables.
The build dates range from 1872 to 2008
The sale dates range from 2006 to 2008
The shape of the data is
(1941, 81)
Numeric Variables
Index(['v_MS_SubClass', 'v_Lot_Frontage', 'v_Lot_Area', 'v_Overall_Qual',
'v_Overall_Cond', 'v_Year_Built', 'v_Year_Remod/Add', 'v_Mas_Vnr_Area',
'v_BsmtFin_SF_1', 'v_BsmtFin_SF_2', 'v_Bsmt_Unf_SF', 'v_Total_Bsmt_SF',
'v_1st_Flr_SF', 'v_2nd_Flr_SF', 'v_Low_Qual_Fin_SF', 'v_Gr_Liv_Area',
'v_Bsmt_Full_Bath', 'v_Bsmt_Half_Bath', 'v_Full_Bath', 'v_Half_Bath',
'v_Bedroom_AbvGr', 'v_Kitchen_AbvGr', 'v_TotRms_AbvGrd', 'v_Fireplaces',
'v_Garage_Yr_Blt', 'v_Garage_Cars', 'v_Garage_Area', 'v_Wood_Deck_SF',
'v_Open_Porch_SF', 'v_Enclosed_Porch', 'v_3Ssn_Porch', 'v_Screen_Porch',
'v_Pool_Area', 'v_Misc_Val', 'v_Mo_Sold', 'v_Yr_Sold', 'v_SalePrice'],
dtype='object')
Categorical Variables
Index(['parcel', 'v_MS_Zoning', 'v_Street', 'v_Alley', 'v_Lot_Shape',
'v_Land_Contour', 'v_Utilities', 'v_Lot_Config', 'v_Land_Slope',
'v_Neighborhood', 'v_Condition_1', 'v_Condition_2', 'v_Bldg_Type',
'v_House_Style', 'v_Roof_Style', 'v_Roof_Matl', 'v_Exterior_1st',
'v_Exterior_2nd', 'v_Mas_Vnr_Type', 'v_Exter_Qual', 'v_Exter_Cond',
'v_Foundation', 'v_Bsmt_Qual', 'v_Bsmt_Cond', 'v_Bsmt_Exposure',
'v_BsmtFin_Type_1', 'v_BsmtFin_Type_2', 'v_Heating', 'v_Heating_QC',
'v_Central_Air', 'v_Electrical', 'v_Kitchen_Qual', 'v_Functional',
'v_Fireplace_Qu', 'v_Garage_Type', 'v_Garage_Finish', 'v_Garage_Qual',
'v_Garage_Cond', 'v_Paved_Drive', 'v_Pool_QC', 'v_Fence',
'v_Misc_Feature', 'v_Sale_Type', 'v_Sale_Condition'],
dtype='object')
Number of unique numerical variables
v_MS_SubClass 16
v_Lot_Frontage 118
v_Lot_Area 1413
v_Overall_Qual 10
v_Overall_Cond 9
v_Year_Built 110
v_Year_Remod/Add 60
v_Mas_Vnr_Area 368
v_BsmtFin_SF_1 787
v_BsmtFin_SF_2 194
v_Bsmt_Unf_SF 938
v_Total_Bsmt_SF 870
v_1st_Flr_SF 901
v_2nd_Flr_SF 508
v_Low_Qual_Fin_SF 23
v_Gr_Liv_Area 1045
v_Bsmt_Full_Bath 3
v_Bsmt_Half_Bath 3
v_Full_Bath 4
v_Half_Bath 3
v_Bedroom_AbvGr 8
v_Kitchen_AbvGr 3
v_TotRms_AbvGrd 13
v_Fireplaces 5
v_Garage_Yr_Blt 99
v_Garage_Cars 5
v_Garage_Area 520
v_Wood_Deck_SF 306
v_Open_Porch_SF 230
v_Enclosed_Porch 147
v_3Ssn_Porch 20
v_Screen_Porch 96
v_Pool_Area 14
v_Misc_Val 28
v_Mo_Sold 12
v_Yr_Sold 3
v_SalePrice 820
dtype: int64
Number of unique categorical variables
parcel 1941
v_MS_Zoning 7
v_Street 2
v_Alley 2
v_Lot_Shape 4
v_Land_Contour 4
v_Utilities 2
v_Lot_Config 5
v_Land_Slope 3
v_Neighborhood 28
v_Condition_1 9
v_Condition_2 8
v_Bldg_Type 5
v_House_Style 8
v_Roof_Style 6
v_Roof_Matl 8
v_Exterior_1st 16
v_Exterior_2nd 17
v_Mas_Vnr_Type 5
v_Exter_Qual 4
v_Exter_Cond 5
v_Foundation 6
v_Bsmt_Qual 5
v_Bsmt_Cond 5
v_Bsmt_Exposure 4
v_BsmtFin_Type_1 6
v_BsmtFin_Type_2 6
v_Heating 6
v_Heating_QC 5
v_Central_Air 2
v_Electrical 5
v_Kitchen_Qual 4
v_Functional 8
v_Fireplace_Qu 5
v_Garage_Type 6
v_Garage_Finish 3
v_Garage_Qual 5
v_Garage_Cond 5
v_Paved_Drive 3
v_Pool_QC 4
v_Fence 4
v_Misc_Feature 5
v_Sale_Type 10
v_Sale_Condition 6
dtype: int64
Main units of observation
v_SalePrice v_Year_Built v_Yr_Sold v_Mo_Sold v_Lot_Area
count 1941.000000 1941.000000 1941.000000 1941.000000 1941.000000
mean 182033.238022 1971.321999 2006.998454 6.431221 10284.770222
std 80407.100395 30.209933 0.801736 2.745199 7832.295527
min 13100.000000 1872.000000 2006.000000 1.000000 1470.000000
25% 130000.000000 1953.000000 2006.000000 5.000000 7420.000000
50% 161900.000000 1973.000000 2007.000000 6.000000 9450.000000
75% 215000.000000 2001.000000 2008.000000 8.000000 11631.000000
max 755000.000000 2008.000000 2008.000000 12.000000 164660.000000
Categorical variable counts
parcel | Note: limited to top 5 values.
1056_528110080 1
1124_528477040 1
1108_528365080 1
1107_528365060 1
1105_528363020 1
Name: parcel, dtype: int64
---
v_MS_Zoning | Note: limited to top 5 values.
RL 1499
RM 320
FV 87
RH 17
C (all) 15
Name: v_MS_Zoning, dtype: int64
---
v_Street | Note: limited to top 5 values.
Pave 1933
Grvl 8
Name: v_Street, dtype: int64
---
v_Alley | Note: limited to top 5 values.
Grvl 82
Pave 54
Name: v_Alley, dtype: int64
---
v_Lot_Shape | Note: limited to top 5 values.
Reg 1213
IR1 661
IR2 55
IR3 12
Name: v_Lot_Shape, dtype: int64
---
v_Land_Contour | Note: limited to top 5 values.
Lvl 1736
HLS 90
Bnk 77
Low 38
Name: v_Land_Contour, dtype: int64
---
v_Utilities | Note: limited to top 5 values.
AllPub 1940
NoSewr 1
Name: v_Utilities, dtype: int64
---
v_Lot_Config | Note: limited to top 5 values.
Inside 1431
Corner 326
CulDSac 119
FR2 53
FR3 12
Name: v_Lot_Config, dtype: int64
---
v_Land_Slope | Note: limited to top 5 values.
Gtl 1850
Mod 81
Sev 10
Name: v_Land_Slope, dtype: int64
---
v_Neighborhood | Note: limited to top 5 values.
NAmes 290
CollgCr 183
OldTown 155
Edwards 129
Somerst 121
Name: v_Neighborhood, dtype: int64
---
v_Condition_1 | Note: limited to top 5 values.
Norm 1674
Feedr 111
Artery 55
RRAn 39
PosN 21
Name: v_Condition_1, dtype: int64
---
v_Condition_2 | Note: limited to top 5 values.
Norm 1918
Feedr 9
Artery 4
PosN 3
PosA 3
Name: v_Condition_2, dtype: int64
---
v_Bldg_Type | Note: limited to top 5 values.
1Fam 1607
TwnhsE 158
Twnhs 66
Duplex 64
2fmCon 46
Name: v_Bldg_Type, dtype: int64
---
v_House_Style | Note: limited to top 5 values.
1Story 968
2Story 581
1.5Fin 212
SLvl 85
SFoyer 54
Name: v_House_Style, dtype: int64
---
v_Roof_Style | Note: limited to top 5 values.
Gable 1543
Hip 356
Gambrel 16
Flat 15
Mansard 7
Name: v_Roof_Style, dtype: int64
---
v_Roof_Matl | Note: limited to top 5 values.
CompShg 1908
Tar&Grv 16
WdShake 7
WdShngl 6
Membran 1
Name: v_Roof_Matl, dtype: int64
---
v_Exterior_1st | Note: limited to top 5 values.
VinylSd 670
MetalSd 308
HdBoard 293
Wd Sdng 277
Plywood 136
Name: v_Exterior_1st, dtype: int64
---
v_Exterior_2nd | Note: limited to top 5 values.
VinylSd 666
MetalSd 310
HdBoard 266
Wd Sdng 263
Plywood 180
Name: v_Exterior_2nd, dtype: int64
---
v_Mas_Vnr_Type | Note: limited to top 5 values.
None 1154
BrkFace 602
Stone 146
BrkCmn 20
CBlock 1
Name: v_Mas_Vnr_Type, dtype: int64
---
v_Exter_Qual | Note: limited to top 5 values.
TA 1201
Gd 658
Ex 65
Fa 17
Name: v_Exter_Qual, dtype: int64
---
v_Exter_Cond | Note: limited to top 5 values.
TA 1704
Gd 187
Fa 41
Ex 8
Po 1
Name: v_Exter_Cond, dtype: int64
---
v_Foundation | Note: limited to top 5 values.
PConc 882
CBlock 813
BrkTil 210
Slab 28
Stone 6
Name: v_Foundation, dtype: int64
---
v_Bsmt_Qual | Note: limited to top 5 values.
TA 847
Gd 817
Ex 168
Fa 57
Po 2
Name: v_Bsmt_Qual, dtype: int64
---
v_Bsmt_Cond | Note: limited to top 5 values.
TA 1723
Gd 93
Fa 70
Ex 3
Po 2
Name: v_Bsmt_Cond, dtype: int64
---
v_Bsmt_Exposure | Note: limited to top 5 values.
No 1227
Av 292
Gd 203
Mn 167
Name: v_Bsmt_Exposure, dtype: int64
---
v_BsmtFin_Type_1 | Note: limited to top 5 values.
Unf 577
GLQ 549
ALQ 292
Rec 197
BLQ 172
Name: v_BsmtFin_Type_1, dtype: int64
---
v_BsmtFin_Type_2 | Note: limited to top 5 values.
Unf 1666
Rec 68
LwQ 61
BLQ 40
ALQ 33
Name: v_BsmtFin_Type_2, dtype: int64
---
v_Heating | Note: limited to top 5 values.
GasA 1913
GasW 18
Grav 4
Wall 3
OthW 2
Name: v_Heating, dtype: int64
---
v_Heating_QC | Note: limited to top 5 values.
Ex 993
TA 553
Gd 333
Fa 59
Po 3
Name: v_Heating_QC, dtype: int64
---
v_Central_Air | Note: limited to top 5 values.
Y 1812
N 129
Name: v_Central_Air, dtype: int64
---
v_Electrical | Note: limited to top 5 values.
SBrkr 1771
FuseA 127
FuseF 34
FuseP 7
Mix 1
Name: v_Electrical, dtype: int64
---
v_Kitchen_Qual | Note: limited to top 5 values.
TA 994
Gd 771
Ex 132
Fa 44
Name: v_Kitchen_Qual, dtype: int64
---
v_Functional | Note: limited to top 5 values.
Typ 1813
Min1 42
Min2 40
Mod 22
Maj1 15
Name: v_Functional, dtype: int64
---
v_Fireplace_Qu | Note: limited to top 5 values.
Gd 504
TA 388
Fa 50
Po 31
Ex 28
Name: v_Fireplace_Qu, dtype: int64
---
v_Garage_Type | Note: limited to top 5 values.
Attchd 1143
Detchd 520
BuiltIn 122
Basment 21
2Types 20
Name: v_Garage_Type, dtype: int64
---
v_Garage_Finish | Note: limited to top 5 values.
Unf 813
RFn 536
Fin 485
Name: v_Garage_Finish, dtype: int64
---
v_Garage_Qual | Note: limited to top 5 values.
TA 1719
Fa 89
Gd 20
Po 4
Ex 2
Name: v_Garage_Qual, dtype: int64
---
v_Garage_Cond | Note: limited to top 5 values.
TA 1758
Fa 50
Gd 14
Po 10
Ex 2
Name: v_Garage_Cond, dtype: int64
---
v_Paved_Drive | Note: limited to top 5 values.
Y 1751
N 147
P 43
Name: v_Paved_Drive, dtype: int64
---
v_Pool_QC | Note: limited to top 5 values.
Ex 4
Gd 4
TA 3
Fa 2
Name: v_Pool_QC, dtype: int64
---
v_Fence | Note: limited to top 5 values.
MnPrv 210
GdPrv 76
GdWo 69
MnWw 10
Name: v_Fence, dtype: int64
---
v_Misc_Feature | Note: limited to top 5 values.
Shed 55
Gar2 4
Othr 2
Elev 1
TenC 1
Name: v_Misc_Feature, dtype: int64
---
v_Sale_Type | Note: limited to top 5 values.
WD 1647
New 201
COD 51
ConLD 16
CWD 12
Name: v_Sale_Type, dtype: int64
---
v_Sale_Condition | Note: limited to top 5 values.
Normal 1551
Partial 205
Abnorml 127
Family 34
Alloca 12
Name: v_Sale_Condition, dtype: int64
---
Graphs
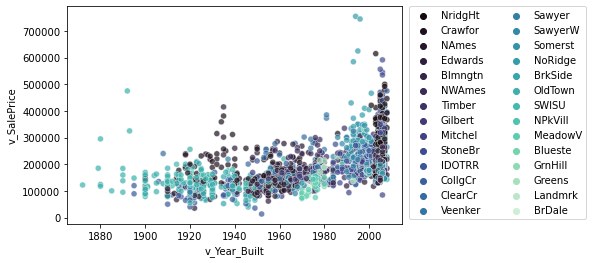
sns.scatterplot(data = df, x = 'v_Year_Built', y = 'v_SalePrice',
hue = 'v_Neighborhood', palette = "mako", alpha = 0.7)
plt.legend(bbox_to_anchor=(1.02, 1), loc='upper left', borderaxespad=0, ncol = 2)
<matplotlib.legend.Legend at 0x7f8ca8a6bee0>
Note - all PairGrid plots have the same hue meanings. Legend will only be displayed for one for brevity.
lot_vars = ['v_Lot_Frontage', 'v_Lot_Area']
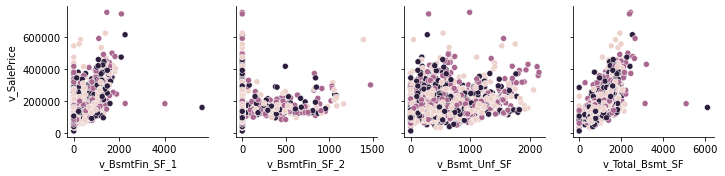
bmnt_vars = ['v_BsmtFin_SF_1', 'v_BsmtFin_SF_2', 'v_Bsmt_Unf_SF', 'v_Total_Bsmt_SF']
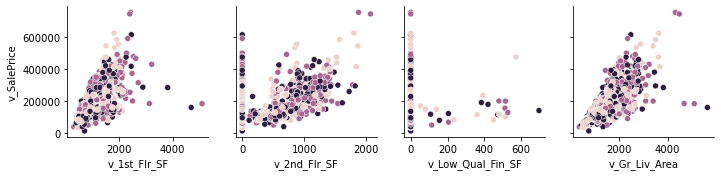
flr_vars = ['v_1st_Flr_SF', 'v_2nd_Flr_SF', 'v_Low_Qual_Fin_SF', 'v_Gr_Liv_Area']
out_vars = ['v_Wood_Deck_SF','v_Open_Porch_SF', 'v_Enclosed_Porch',
'v_3Ssn_Porch', 'v_Screen_Porch']
a = sns.PairGrid(df, x_vars = lot_vars, y_vars = 'v_SalePrice', hue = 'v_Yr_Sold')
a.map(sns.scatterplot)
a.add_legend()
<seaborn.axisgrid.PairGrid at 0x7f8c912ac6a0>
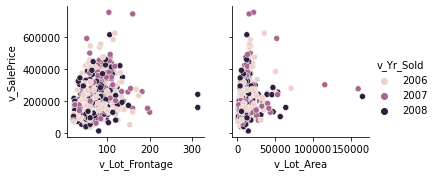
b = sns.PairGrid(df, x_vars = bmnt_vars, y_vars = 'v_SalePrice', hue = 'v_Yr_Sold')
b.map(sns.scatterplot)
<seaborn.axisgrid.PairGrid at 0x7f8c907e9af0>
c = sns.PairGrid(df, x_vars = flr_vars, y_vars = 'v_SalePrice', hue = 'v_Yr_Sold')
c.map(sns.scatterplot)
<seaborn.axisgrid.PairGrid at 0x7f8c916df760>
b = sns.PairGrid(df, x_vars = out_vars, y_vars = 'v_SalePrice', hue = 'v_Yr_Sold')
b.map(sns.scatterplot)
<seaborn.axisgrid.PairGrid at 0x7f8c913f1d90>
sns.displot(data = df, x = 'v_Mo_Sold', kind = 'kde', hue = 'v_Yr_Sold')
<seaborn.axisgrid.FacetGrid at 0x7f8c916df5e0>
sns.boxplot(data = df, x = 'v_Bldg_Type', y = 'v_SalePrice')
<AxesSubplot:xlabel='v_Bldg_Type', ylabel='v_SalePrice'>
sns.boxplot(data = df, x = 'v_Lot_Shape', y = 'v_SalePrice')
<AxesSubplot:xlabel='v_Lot_Shape', ylabel='v_SalePrice'>
sns.boxenplot(data = df, x = 'v_SalePrice', y = 'v_Functional')
<AxesSubplot:xlabel='v_SalePrice', ylabel='v_Functional'>
Part 2: Running Regressions
Run these regressions on the RAW data, even if you found data issues that you think should be addressed.
Insert cells as needed below to run these regressions. Note that $i$ is indexing a given house, and $t$ indexes the year of sale.
- $\text{Sale Price}_{i,t} = \alpha + \beta_1 * \text{v_Lot_Area}$
- $\text{Sale Price}_{i,t} = \alpha + \beta_1 * log(\text{v_Lot_Area})$
- $log(\text{Sale Price}_{i,t}) = \alpha + \beta_1 * \text{v_Lot_Area}$
- $log(\text{Sale Price}_{i,t}) = \alpha + \beta_1 * log(\text{v_Lot_Area})$
- $log(\text{Sale Price}_{i,t}) = \alpha + \beta_1 * \text{v_Yr_Sold}$
- $log(\text{Sale Price}_{i,t}) = \alpha + \beta_1 * (\text{v_Yr_Sold==2007})+ \beta_2 * (\text{v_Yr_Sold==2008})$
- Choose your own adventure: Pick any five variables from the dataset that you think will generate good R2. Use them in a regression of $log(\text{Sale Price}_{i,t})$
- Tip: You can transform/create these five variables however you want, even if it creates extra variables. For example: I’d count Model 6 above as only using one variable:
v_Yr_Sold. - I got an R2 of 0.877 with just “5” variables. How close can you get? I won’t be shocked if someone beats that!
- Tip: You can transform/create these five variables however you want, even if it creates extra variables. For example: I’d count Model 6 above as only using one variable:
Bonus formatting trick: Instead of reporting all regressions separately, report all seven regressions in a single table using summary_col.
Assignment Regressions
# regressions
# assignment regressions
reg1 = sm_ols('v_SalePrice ~ v_Lot_Area', data = df).fit()
reg2 = sm_ols('v_SalePrice ~ np.log(v_Lot_Area)', data = df).fit()
reg3 = sm_ols('np.log(v_SalePrice) ~ v_Lot_Area', data = df).fit()
reg4 = sm_ols('np.log(v_SalePrice) ~ np.log(v_Lot_Area)', data = df).fit()
reg5 = sm_ols('np.log(v_SalePrice) ~ v_Yr_Sold', data = df).fit()
reg6 = sm_ols('np.log(v_SalePrice) ~ (v_Yr_Sold == 2007) + (v_Yr_Sold == 2008)', data = df).fit()
# creating extra outputs
info_dict={'R-squared' : lambda x: f"{x.rsquared:.3f}",
'Adj R-squared' : lambda x: f"{x.rsquared_adj:.3f}",
'No. observations' : lambda x: f"{int(x.nobs):d}"}
# creating output table
print('='*101)
print(' y = Sale Price not specified, log(Sale Price) else')
print(summary_col(results = [reg1, reg2, reg3, reg4, reg5, reg6],
float_format = '%0.3f',
stars = True,
model_names = ['Price1', 'Price2', '(log)Price1',
'(log)Price2', '(log)Price3', '(log)Price4'],
info_dict=info_dict ,
regressor_order = ['Intercept', 'v_Lot_Area', 'np.log(v_Lot_Area)',
'v_Yr_Sold']
)
)
=====================================================================================================
y = Sale Price not specified, log(Sale Price) else
======================================================================================================
Price1 Price2 (log)Price1 (log)Price2 (log)Price3 (log)Price4
------------------------------------------------------------------------------------------------------
Intercept 154789.550*** -327915.802*** 11.894*** 9.405*** 22.293 12.023***
(2911.591) (30221.347) (0.015) (0.151) (22.937) (0.016)
v_Lot_Area 2.649*** 0.000***
(0.225) (0.000)
np.log(v_Lot_Area) 56028.170*** 0.288***
(3315.139) (0.017)
v_Yr_Sold -0.005
(0.011)
v_Yr_Sold == 2007[T.True] 0.026
(0.022)
v_Yr_Sold == 2008[T.True] -0.010
(0.023)
R-squared 0.067 0.128 0.065 0.135 0.000 0.001
R-squared Adj. 0.066 0.128 0.064 0.135 -0.000 0.000
R-squared 0.067 0.128 0.065 0.135 0.000 0.001
Adj R-squared 0.066 0.128 0.064 0.135 -0.000 0.000
No. observations 1941 1941 1941 1941 1941 1941
======================================================================================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01
Exploratory Regression
reg7 = sm_ols('np.log(v_SalePrice) ~ v_Gr_Liv_Area + C(v_Bldg_Type) + C(v_Exter_Cond) + C(v_MS_Zoning) + C(v_Condition_1)',
data = df).fit()
print(reg7.summary())
OLS Regression Results
===============================================================================
Dep. Variable: np.log(v_SalePrice) R-squared: 0.669
Model: OLS Adj. R-squared: 0.665
Method: Least Squares F-statistic: 168.4
Date: Sun, 02 Apr 2023 Prob (F-statistic): 0.00
Time: 18:01:12 Log-Likelihood: 80.935
No. Observations: 1941 AIC: -113.9
Df Residuals: 1917 BIC: 19.83
Df Model: 23
Covariance Type: nonrobust
=============================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------------------
Intercept 10.8666 0.251 43.207 0.000 10.373 11.360
C(v_Bldg_Type)[T.2fmCon] -0.1028 0.036 -2.845 0.004 -0.174 -0.032
C(v_Bldg_Type)[T.Duplex] -0.2638 0.030 -8.804 0.000 -0.323 -0.205
C(v_Bldg_Type)[T.Twnhs] -0.0577 0.031 -1.870 0.062 -0.118 0.003
C(v_Bldg_Type)[T.TwnhsE] 0.2096 0.021 10.171 0.000 0.169 0.250
C(v_Exter_Cond)[T.Fa] -0.3716 0.091 -4.080 0.000 -0.550 -0.193
C(v_Exter_Cond)[T.Gd] -0.1367 0.084 -1.618 0.106 -0.302 0.029
C(v_Exter_Cond)[T.Po] -1.9712 0.344 -5.725 0.000 -2.646 -1.296
C(v_Exter_Cond)[T.TA] -0.1291 0.083 -1.555 0.120 -0.292 0.034
C(v_MS_Zoning)[T.C (all)] -0.1206 0.245 -0.491 0.623 -0.602 0.361
C(v_MS_Zoning)[T.FV] 0.4442 0.240 1.852 0.064 -0.026 0.914
C(v_MS_Zoning)[T.I (all)] -0.3407 0.334 -1.021 0.308 -0.995 0.314
C(v_MS_Zoning)[T.RH] 0.1578 0.245 0.643 0.520 -0.324 0.639
C(v_MS_Zoning)[T.RL] 0.3774 0.238 1.583 0.113 -0.090 0.845
C(v_MS_Zoning)[T.RM] 0.1115 0.238 0.468 0.640 -0.356 0.579
C(v_Condition_1)[T.Feedr] 0.0630 0.039 1.605 0.109 -0.014 0.140
C(v_Condition_1)[T.Norm] 0.2123 0.033 6.457 0.000 0.148 0.277
C(v_Condition_1)[T.PosA] 0.2457 0.073 3.378 0.001 0.103 0.388
C(v_Condition_1)[T.PosN] 0.2381 0.061 3.922 0.000 0.119 0.357
C(v_Condition_1)[T.RRAe] 0.1728 0.062 2.807 0.005 0.052 0.294
C(v_Condition_1)[T.RRAn] 0.1916 0.050 3.864 0.000 0.094 0.289
C(v_Condition_1)[T.RRNe] 0.1542 0.121 1.272 0.204 -0.084 0.392
C(v_Condition_1)[T.RRNn] 0.4033 0.121 3.328 0.001 0.166 0.641
v_Gr_Liv_Area 0.0005 1.04e-05 48.837 0.000 0.000 0.001
==============================================================================
Omnibus: 434.494 Durbin-Watson: 1.534
Prob(Omnibus): 0.000 Jarque-Bera (JB): 4314.341
Skew: -0.758 Prob(JB): 0.00
Kurtosis: 10.145 Cond. No. 2.07e+05
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.07e+05. This might indicate that there are
strong multicollinearity or other numerical problems.
Part 3: Regression interpretation
Insert cells as needed below to answer these questions. Note that $i$ is indexing a given house, and $t$ indexes the year of sale.
- If you didn’t use the
summary_coltrick, list $\beta_1$ for Models 1-6 to make it easier on your graders. - Interpret $\beta_1$ in Model 2.
- Interpret $\beta_1$ in Model 3.
- HINT: You might need to print out more decimal places. Show at least 2 non-zero digits.
- Of models 1-4, which do you think best explains the data and why?
- Interpret $\beta_1$ In Model 5
- Interpret $\alpha$ in Model 6
- Interpret $\beta_1$ in Model 6
- Why is the R2 of Model 6 higher than the R2 of Model 5?
- What variables did you include in Model 7?
- What is the R2 of your Model 7?
- Speculate (not graded): Could you use the specification of Model 6 in a predictive regression?
- Speculate (not graded): Could you use the specification of Model 5 in a predictive regression?
Question 1
Not Applicable
Question 2
reg2.summary()
y10000 = reg2.params[0]+np.log(10000)*reg2.params[1]
y10100 = reg2.params[0]+np.log(10100)*reg2.params[1]
print(f"""Reg 2:
intercept: {reg2.params[0]}
beta1: {reg2.params[1]}
y at lot size == 10000: {y10000}
y at lot size == 10100: {y10100}
Going from lot size 10000 to 10100, reg2 predicts sale price change of: {y10100-y10000}
""")
print("A 1% increase in lot area is associated with a sales price increase of roughly", reg2.params[1]/100, "dollars.")
Reg 2:
intercept: -327915.8023202382
beta1: 56028.169960465355
y at lot size == 10000: 188122.71343457908
y at lot size == 10100: 188680.2122627832
Going from lot size 10000 to 10100, reg2 predicts sale price change of: 557.4988282041159
A 1% increase in lot area is associated with a sales price increase of roughly 560.2816996046536 dollars.
Question 3
reg3.summary()
print(f"""Reg 3:
intercept: {reg3.params[0]}
beta1: {reg3.params[1]}
""")
print("A 1 unit increase in lot area is associated with a sales price increase of ", 100 * (np.exp(reg3.params[1])-1), "percent.")
Reg 3:
intercept: 11.89407251466273
beta1: 1.3092338465836551e-05
A 1 unit increase in lot area is associated with a sales price increase of 0.001309242417080192 percent.
Question 4
Model 4 seems to be the model that best explains the data. It has the highest R2 of the four models, meaning the beta is more reliable.
Question 5
reg5.summary()
print(f"""Reg 5:
intercept: {reg5.params[0]}
beta1: {reg5.params[1]}
""")
print("A 1 year increase in sale year is associated with a sales price decrease of ", 100 * (np.exp(reg5.params[1])-1), "percent.")
Reg 5:
intercept: 22.293213132062135
beta1: -0.005114348195977281
A 1 year increase in sale year is associated with a sales price decrease of -0.5101292184388373 percent.
Question 6
The alpha in model 6 is ~12.023. This means the average value of log(SalesPrice) is ~12.023 for group zero (The intercept X = 0)
Question 7
reg6.summary()
print(f"""Reg 6:
intercept: {reg6.params[0]}
beta1: {reg6.params[1]}
beta2: {reg6.params[2]}
""")
print("The year 2007 is asscociated with a sales price change of ", 100 * (np.exp(reg6.params[1])-1), "percent. Ceterus Parisbus.", "\n",
"The year 2008 is asscociated with a sales price change of ", 100 * (np.exp(reg6.params[2])-1), "percent. Ceterus Parisbus.")
Reg 6:
intercept: 12.022869210751946
beta1: 0.025590319971648456
beta2: -0.010281565074492738
The year 2007 is asscociated with a sales price change of 2.5920563202177727 percent. Ceterus Parisbus.
The year 2008 is asscociated with a sales price change of -1.0228890464679674 percent. Ceterus Parisbus.
Question 8
The R-squared of model 6 is higher than the R-squared of model 5 because model 6 is categorically separated, while model 5 the years are being treated like a continuous variable.
Question 9
For my exploratory regression I choose to use multiple categorical variables as well as a few continuous variables. For the y variable I used the log of the sales price per instructions. My X variables included: the size of the general living area, the building type, the exterior condition of the house, the zoning type of the land, and the first set of house conditions. </br> The explicit variable names are:
X = ['v_Gr_Liv_Area', 'v_Bldg_Type', 'v_Exter_Cond', 'v_MS_Zoning', 'v_Condition_1']
y = 'v_SalePrice'
Question 10
The R-squared of my model is 0.669.
Question 11
No you cannot use the specification of model 6 as a predictive regression because you are modeling based on the sale year. Every year the sale year will change simply because time moved forward.
Question 12
No you cannot use the specification of model 5 as a predictive regression because of the aforementioned issue in Q11 and this model is not separated categorically so the years are treated as continuous variables.